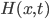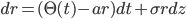Short Rate

On the Design Board: From Single- to Multi-Curve

Posted on April 18, 2016 by Michele Maio

Introduction

Standard fixed-income applications make a larger and larger use of the multi-curve framework to price products and hedge risks. For whatever reason this is the case, it is useful to know how to implement such a framework.

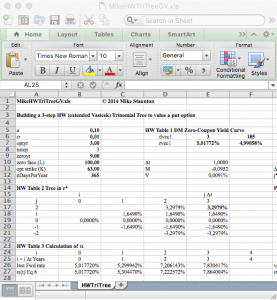
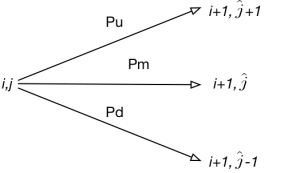
We have already talked about multi-curves in the past. Here we gave a list useful references and here we illustrated the mean features of risk metrics and sensitivity patterns. In this blog, we describe how to design the multi-curve framework. We do not claim that this is the only way or the best way. This is one possible way, which however turned out to work quite well within our system and happened to be easily integrated into our library.

Code snippets that will be shown below have been developed in C# using Visual Studio. Continue reading →

Theta - Critical Note

Posted on February 12, 2016 by Jorrit de Jong

In a previous blog we presented an implementation of the Generalised Hull-White model (2014). This implementation relies on a numerical root-finding routine to determine model parameters so that model prices match actual market prices. The root finding is far from trivial as different algorithms will give different results. Fortunately the quality of the result can be easily monitored as the difference between model prices and actual marked prices is a clear indicator. As it turns out in most cases, the root finding for theta is not required. Instead an analytical formula can be used. Mike Staunton very kindly pointed us to a paper by Grant & Vora (2001) that shows that the approximation used by Hull-White is not necessary. The equations explained in the paper are implemented in the attached spreadsheet by Mike Stauton for the first 3 steps of the lattice giving a good example of how the process for finding theta works in practice.

The spreadsheet is available here:

MikeHWTriTreeGV

References:

Grant & Vora (2001) , An Analytical Implementation of the Hull and White Model

http://janroman.dhis.org/finance/Hull%20&%20White/analytical-approximation-hull-and-white.pdf

Hull & White (2014), A Generalized Procedure for Building Trees for the Short Rate and its

Application to Determining Market Implied Volatility Functions

http://www-2.rotman.utoronto.ca/~hull/downloadablepublications/TreeBuilding.pdf

Review of Lattice Construction Methods

Posted on December 30, 2015 by Jorrit de Jong

Just before year end we put out our paper, titled "Review of Lattice Construction Methods"!

This paper extends the generalized procedure for building trees for short rates by Hull & White. A generalization for any mean and standard deviation of the underlying short rate model is presented. In addition we review the methodologies for constructing lattice models and give a step-by-step explanation on how to construct trinominal trees. We apply the formalism to some explicit examples of various complexity.

Full text can be found here

Theta : A Test for Short Rate Model Lattice

Posted on April 3, 2015April 5, 2016 by Jorrit de Jong

While short rate models have lost ground to libor market models for valuation of (complex) interest rate derivatives, they remain popular for Asset and Liability Management. As a result you may find yourself implementing a short rate model. Often the choice is to implement a lattice approach, perhaps in combination with a Monte Carlo framework. One critical step in these models is to match the model discounts to the ones observed in the market. This makes to model (almost) arbitrage free. To match the market a numerical root finding algorithm needs to be used, for example Newton Raphson. This poses the challenge that mistakes in the model may not be obvious as the root finder can still find parameters to match the market even though there are mistakes in the model. Our suggestion is to check the root finder solution to known analytical solution of the Hull White model using functional form for the zero curve that is continuous and two times differentiable.

Continue reading →

Generalized Procedure for Building Short Rate Trees in Excel / VBA using LevmarExcel

Posted on February 13, 2015April 5, 2016 by Jorrit de Jong

In a previous we blog we reproduced example 1 of the 2014 paper John Hull and Alan White “Generalized Procedure for Building Short Rate Trees”. In the paper the authors derive a generalized method for the construction of short rate trees. This generalization is interesting as it allows for one tree (or lattice) construction algorithm for all one-factor short rate models. Continue reading →

Generalized Procedure for Building Short Rate Trees in Excel / VBA

Posted on January 20, 2015September 25, 2015 by Jorrit de Jong

In their 2014 paper John Hull and Alan White derive generalized method for the construction of short rate trees. This generalization is interesting as it allows for one tree (or lattice) construction algorithm for all one factor short rate models. The only difference between the various models is the function , which is explained briefly here and in detail in the paper. Continue reading →

Reproduction Example 1 of Generalized Procedure for Building Trees

Posted on December 21, 2014September 25, 2015 by Jorrit de Jong

In a recent (2014) paper John Hull and Alan White demonstrate a generalized method for the construction of short rate trees. Keen to understand the model we tried to reproduce the results of the first example mentioned in the paper on page 10. The example considers the short rate model:

which is transformed using