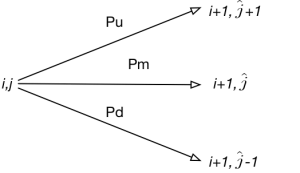
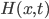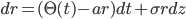Just before year end we put out our paper, titled "Review of Lattice Construction Methods"!
This paper extends the generalized procedure for building trees for short rates by Hull & White. A generalization for any mean and standard deviation of the underlying short rate model is presented. In addition we review the methodologies for constructing lattice models and give a step-by-step explanation on how to construct trinominal trees. We apply the formalism to some explicit examples of various complexity.
Full text can be found here