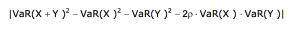We have recently finished a project with an international insurer whose headquarters is in the Netherlands Randstad area. The experience was extremely satisfactory, mainly due to the interactions with the quant development group, which was very knowledgable and provided a pleasant working environment, and the topic under investigation, which was the construction of a system to compute economic capital requirements of the firm. Hence it is interesting to remind ourselves of some of the regulatory requirements behind the insurance business.
Generically, economic capital requirements are attached to the solvency word, which denotes the degree to which assets exceed liabilities. The difference (if positive) is also known as own funds. Such Solvency Capital Requirements (SCR in short) are dictated the European Insurance and Occupational Pensions Authority (EIOPA), which will be referred to as the regulator in the rest of this post. In mathematical terms, capital requirements are Values at Risk (VaR's), hence variances at given confidence levels.
One such regulatory requirement is known as the Standard Formula. As the name suggests, this is a standardised calculation that all the firms are asked to implement. However, it might not exactly reflect the risk profile of any specific entity and moreover, some risks might be relevant for some entities only, while completely irrelevant for others. Our main reference for this post will be the original EIOPA documentation which can be found here or here.
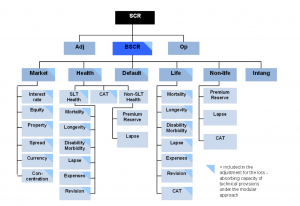
In the the Standard Formula calculations the various sources of risks are organised into a hierarchical structure (see picture). The root node represents the Basic Solvency Capital Requirement (BSCR) for the whole firm.
A capital requirement is calculated for each module in the risk hierarchy. All the capital requirements at each level are then aggregated into the parent level by using correlation matrices. The correlation parameters are chosen in such a way that the calculated SCR best approximates the 99.5% VaR over a one-year period of the aggregated capital requirement. In formulas, for two risk factors X and Y, the correlation parameter rho minimises the absolute difference:
Let's now look at each risk source in more details. Continue reading