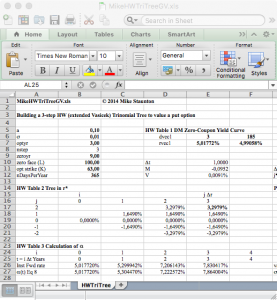
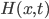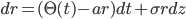In a previous blog we presented an implementation of the Generalised Hull-White model (2014). This implementation relies on a numerical root-finding routine to determine model parameters so that model prices match actual market prices. The root finding is far from trivial as different algorithms will give different results. Fortunately the quality of the result can be easily monitored as the difference between model prices and actual marked prices is a clear indicator. As it turns out in most cases, the root finding for theta is not required. Instead an analytical formula can be used. Mike Staunton very kindly pointed us to a paper by Grant & Vora (2001) that shows that the approximation used by Hull-White is not necessary. The equations explained in the paper are implemented in the attached spreadsheet by Mike Stauton for the first 3 steps of the lattice giving a good example of how the process for finding theta works in practice.
The spreadsheet is available here:
References:
Grant & Vora (2001) , An Analytical Implementation of the Hull and White Model
http://janroman.dhis.org/finance/Hull%20&%20White/analytical-approximation-hull-and-white.pdf
Hull & White (2014), A Generalized Procedure for Building Trees for the Short Rate and its
Application to Determining Market Implied Volatility Functions
http://www-2.rotman.utoronto.ca/~hull/downloadablepublications/TreeBuilding.pdf