While short rate models have lost ground to libor market models for valuation of (complex) interest rate derivatives, they remain popular for Asset and Liability Management. As a result you may find yourself implementing a short rate model. Often the choice is to implement a lattice approach, perhaps in combination with a Monte Carlo framework. One critical step in these models is to match the model discounts to the ones observed in the market. This makes to model (almost) arbitrage free. To match the market a numerical root finding algorithm needs to be used, for example Newton Raphson. This poses the challenge that mistakes in the model may not be obvious as the root finder can still find parameters to match the market even though there are mistakes in the model. Our suggestion is to check the root finder solution to known analytical solution of the Hull White model using functional form for the zero curve that is continuous and two times differentiable.

For the construction of the lattice we use the approach as described in Hull & White (2001). The paper constructs the lattice in 4 steps:

1. Fix the timesteps for the lattice
2. Fix the step size of the underlying Ornstein Uhlenbeck
3. Choose branching process
4. Adjust the lattice to match market (implied) discounts

For the Hull White model we have

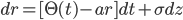
Which can be written as

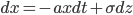
and

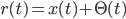
The model discounts are given by formula 6 in the 2001 paper:

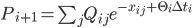
Next, we use a numerical search algorithm to find the that makes the model discounts the same as the ones observed in the market. Later it is shown that this approach can be generalised for other short rate models.

The market discounts are simulated using the zero rate curve suggested in Pelsser(1998)

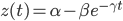
which implies the market discounts to be

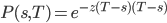
For the Hull White model an analytical expression for is known (see Hull 2014)

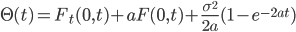
Where F(0,t) is the instantaneous forward rate and F_t its derivative with respect to t. These can be computed as follows:

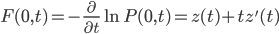
and its derivative

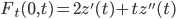
with

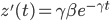
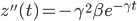
We can now compare the analytical and numerical solutions and confirm that the lattice implementation results in reasonable values. An example of errors we found during our experiments is given here:

Having tested the geometry of the lattice construction algorithm, we can now generalise the expressions used to fit other short rate models. The underlying lattice for the Ornstein Uhlenbeck process is kept the same, but we change the functions

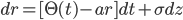
and

 

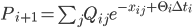
into

 

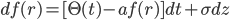
and

 

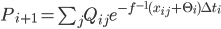
In this way the general set up of the original paper is recovered, but now with a sanity check to validate the numerical results of the root finding of

In conclusion, this blog shows a way to check a general lattice implement for the case of Hull White short rate. This test is advised as numerical root finding may cloud any issues in the optimisation you may be facing.

 

References:

Clewlow & Strickland (1998), Implementing Derivative Models, Wiley
http://eu.wiley.com/WileyCDA/WileyTitle/productCd-0471966517.html

Hull & White (2001), The General Hull-White Model and Super Calibration
http://www-2.rotman.utoronto.ca/~hull/DownloadablePublications/Generalized%20HW%20model%20and%20Super%20Calibration.pdf

Hull (2014), Options, Futures, and Other Derivatives, Ninth Edition,Prentice Hall
http://www-2.rotman.utoronto.ca/~hull/ofod/index.html

Pelsser (1998), Efficient Methods for Valuing Interest Rate Derivative, Springer
http://www.springer.com/gp/book/9781852333041