In a recent (2014) paper John Hull and Alan White demonstrate a generalized method for the construction of short rate trees. Keen to understand the model we tried to reproduce the results of the first example mentioned in the paper on page 10. The example considers the short rate model:
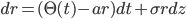
which is transformed using
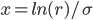
into
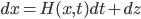
with
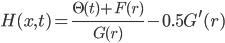 .
.
In case of the example we use
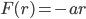
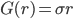
To keep things as simple as possible we only consider the first theta here, which allows us to do all the computations on the spreadsheet without resorting to VBA or embedded libraries (currently we are working on a standalone code that will implement the complete tree building algorithm using VBA which will be posted here once completed).
The spreadsheet is organised in four sections or steps:
- Step one takes the input data
- Step two lists the x and rates that make up the tree
- Step three computes the probabilities in each node. A node can be selected by entering its coordinate in cell D68 and D69.
- Finally, step four gives the discount in the first node. This discount should correspond to the input rates.
Consider the first node. In this spreadsheet we can find the theta that makes the initial discount equal to the one based on the input data using goal seek. We do so by computing the discount based on the input as:
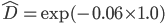
The discount based on the lattice is:
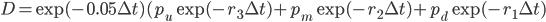
where

(for this specific model choice).
Now define the error function
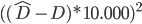 .
.
Minimization using goal seek in Excel 2011 returns a theta equal to 0,0498165.
The spreadsheet is available here:
Reference:
A Generalized Procedure for Building Trees for the Short Rate and its Application to Determining Market Implied Volatility Functions
By
John Hull and Alan White
And is available here:
http://www-2.rotman.utoronto.ca/~hull/downloadablepublications/TreeBuilding.pdf