How can we hedge within the multi-curve framework?

Let’s consider a simplified case. Our building blocks will be swaps only of various tenors and maturities with the following purposes:

• Discounting instruments: we use 1-month tenor swaps of various maturities to construct the discounting curve.
• Tenor instruments: we use 3-months, 6-months and 12-months tenor swaps to construct the forward curves. We denote them as 3M, 6M and 12M.

The exact swap data are given in the attached spreadsheets [a] and [b]. In particular:

• the Data tab contains details of the input data and convention used in the calculation;
• the Rows tab contains the matrix with the PV01s/IV01s of all the input instruments as rows;
• the Columns tab contains the actual PV01/IV01 matrices as the transpose of the matrix in the previous tab;
• our notation in these examples is that all the curves are ordered by discounting type (the first one is always the discounting curve) and increasing tenors.

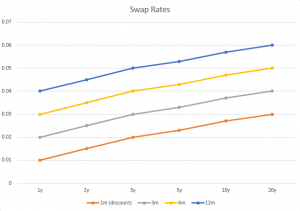
The picture bellows provides a graphical illustration of the input swap instruments used to bootstrap discount curve and all the tenor curves as extracted from the Data tab.

With the above data we can construct the multi-curve, i.e. the set of discount curve as well as all the tenor curves.

Constructing the discount curve is simply a matter of applying the single-curve framework to the discounting instruments. Once this curve has been computed, we must use it to bootstrap all the other curves from the instruments of given tenor.

What about sensitivities?

In a previous paper [1], we presented the analytical formulas for IV01 (instrument value of 1bp) and PV01 (present value of 1bp) matrices and showed how these two quantities are related by a change of coordinates. Here we do the same in the multi-curve framework but at numerical level.

Sensitivities of a product are studied by bumping all the rates that are relevant for pricing that product. Typical bumps are of 1bp. Such rates can be either zero or instrument rates of the underlying curves. Then we obtain the PV01 and IV01 vectors respectively.

We can repeat the same procedure and work out the PV01 and IV01 vectors for each instrument used in the multi-curve bootstrap. Then we can organise these vectors as columns of square matrices. Such matrices are simply the PV01 and IV01 matrices in the multi-curve framework.

What is the shape of such matrices?

In the single-curve framework we already know that they are upper triangular. Moreover, the main contribution is on the diagonal. Our intuition tells us that this structure should be readily generalized to the multi-curve framework. In this case, in fact, we expect that these matrices will be still upper triangular. In addition, they should have a block structure where each sub-block is also upper triangular, with some of the blocks being equal to zero.

In fact, when bootstrapping any of the tenor curves, the only instruments that are relevant are the discounting instruments and the tenor instruments for the corresponding curve. In this example with standard interest-rate swaps, we expect no effect when we bump instruments belonging to a different tenor curve Things gets more interesting when float-float swaps are added to the picture. We will come back to these cases in the future.

Our expectations are confirmed by the numerical studies, which are presented in the attached spreadsheets.

To summarize

Problem: hedging with multi-curve

Solution: follow your intuition

Attachments

[a] Spreadsheet with PV01 matrix: PV01 matrix

[b] Spreadsheet with IV01 matrix: IV01 matrix

References

[1] M. Maio, J. J. de Jong (2014), The Geometry of Interest Rate Risk, PRE-PRINT UD 2014-02