Introduction
One of the most interesting things about financial engineering is that it’s not just another domain.  On top of all the problems associated software engineering, financial engineers also have to deal with the problems of their traditional home ground.  I.e. have to fix real financial problems.

To find to optimal hedging ratio involves a couple of steps. Next week I want to take my students  through the motions. To demonstrate the effect correlation of the underlying assets has on a hedging strategy a stylised model is considered. Therefore I thought it would be worth to write up my notes and stick it on the website.

Model

A model of a single portfolio is considered with a known variance and size. To hedge the risk, e.g. reduce the variance, of the portfolio only one assets is available. This assets is called the hedge instrument. The variance and correlation with the portfolio of hedge instrument is known. Historic data could be used to compute the relevant variances and correlation or one could opt to use current market consensus.

The size of portfolio to be hedged is given by 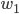and has a standard deviation of 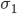. To hedge this portfolio the hedge instrument is going to be used. The hedge instrument size is given by 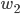and has a standard deviation of 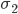. The correlation between the portfolio to be hedged and the hedge instrument is given by 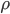. Based on the above the variance of the portfolio can be computed to be:

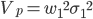  (1)

A similar computation of variance can be made for the portfolio with the hedge instrument added to the mix. The hedge instrument is added to reduce variance or eliminate it all together. Computing the total variance yields:

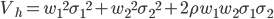(2)

The weight of the portfolio to be hedged can be chosen arbitrary with out of lose of generality. However which position should be taken in the hedge instrument to reduce the total variance the most? For this the optimal hedge ratio has to be computed. To find the optimum for the hedge instrument the derivative is computed:

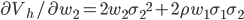    (3)

To find the optimal position in the hedge instrument set equation ref{eq:derivative} equal zero and solve for 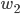. This position is called the optimal hedge ratio and is give by:

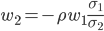     (4)

A similar results can be found in literature for example in Hull (2005) or Kocken (1997).
The impact of using the optimal hedge ratio is computed by substituting the optimal hedge ratio (equation 4) in the variance of the total portfolio (equation 2), this leads to:

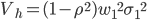     (5)

The hedge effectivity measures how effectively the suggested strategy reduces variance compared to the original unhedged portfolio. The hedge effectivity is the relative variance in the hedged portfolio compared to the original unhedged portfolio multiplied by minus one. Since a reduction in variance is the goal of hedging it should show up in the results as a large positive number, hence the multiplication with minus one.

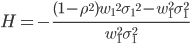    (6)

Rearranging the equation leads to

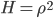     (7)

Analysis
The proposed hedging strategy using the optimal hedging ratio can be compared to a less optimal, but very illustrative case. Consider a hedger using:

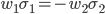     (8)

The variance of the portfolio including hedge is given by:

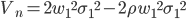   (9)

This case is clearly optimal when there is complete correlation between the portfolio to be hedged and the hedge instrument. Given a correlation of one the variance of the total position would be eliminated. However once correlation drops this hedge deteriorates quickly, linearly in correlation, this strategy will be called the linear strategy. By computing the hedge effectivity it becomes apparent that the linear strategy earns its name.

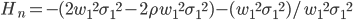    (10)

Rearranging the equation leads to:

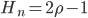     (11)

Putting the two options side by side produces graph1. From the graph it is clear that the two strategies yield the same reduction in variance when correlation between the portfolio to be hedged and the hedge instrument is prefect. Once correlation drops to 0.5 the linear strategy does not yield any variance reduction, while the optimal strategy still produce some reduction is variance.

Consider the case were there is no correlation between the portfolio to be hedged and the hedge instrument. The optimal hedge ratio is now zero, implying it is best to do no hedging at all for the optimal strategy. The linear strategy does set up an hedge and in doing so doubles variance!

Once variance becomes negative the difference between the two strategies becomes very apparent. The parabolic shape of the optimal hedge ratio starts making sense. If correlation is negative simply take a short position equal to long position that would be take if correlation would have had a positive sign. The linear strategy was not designed for negative correlation and will not be considered here.

Conclusion
Using a simple model it was shown that various hedging strategies can greatly influence the total variance reduction achieved, illustrating that setting up a hedge should be subject to deep thought.

In our case an optimal hedging ratio was found for a simple model. There is no reason why this same technique wouldn't work form more complicated models.
The hedging effectivity was introduced as a general way to evaluate the effectivenes of a hedge.

References
Hull, J. C. (2005), Options, Futures and Other Derivatives (6th Edition), Prentice Hall
Kocken, T. (1997), Financial Risk Management, Tutein Nolthenius

originally posted on http://archive.uglyduckling.nl/financialagile/finance/optimal-hedge-ratio/.