Here we share our current projects, research ideas, events, news and anything else that comes out of our brainstorming sessions
Ugly Duckling was lucky to grab Ugly Duckling dot IT domain name. We are very happy to have added this new channel to our online footprint and thus becoming part of the first top level domain in Europe. With 2.5 million registered domains it is the 16th largest domain out there.
Standard fixed-income applications make a larger and larger use of the multi-curve framework to price products and hedge risks. For whatever reason this is the case, it is useful to know how to implement such a framework.
We have already talked about multi-curves in the past. Here we gave a list useful references and here we illustrated the mean features of risk metrics and sensitivity patterns. In this blog, we describe how to design the multi-curve framework. We do not claim that this is the only way or the best way. This is one possible way, which however turned out to work quite well within our system and happened to be easily integrated into our library.
Code snippets that will be shown below have been developed in C# using Visual Studio. Continue reading
Tapestry 5 is framework for creating web applications using Java. The framework allows you to generate HTML pages using Java code. This a good thing if you have complex business logic that takes data from the user, database, online resources to present a result as a webpage. We wanted to do something like that for one of our econometric models so we decided to give Tapestry a go for building our web application. Along the way we learned quite a lot about the framework. Some of that we want to share here in a series of blogs. The complete series should be enough to build simple GUI for your Java business logic.
In this blog we will create a hello-world style example using Tapestry 5. The goal of this example is to get you up and running with Tapestry using the skeleton setup that is included with Tapestry. Based on this initial setup we will make changes to get a hello-world page.
Prerequisites
Let’s consider a simplified case. Our building blocks will be swaps only of various tenors and maturities with the following purposes:
The exact swap data are given in the attached spreadsheets [a] and [b]. In particular:
In this blog we consider the hazard (or default) rate implied by Credit Default Swaps (CDS). In specific we compare a simplified CDS-spreads-based model against a bootstrap procedure. Surprisingly we find that the simplified approach works well in the current low-interest rate market. Our findings are based on a piecewise linear hazard rate curve. The nodes for these curves are obtained using either the simple model or the bootstrap approach.
We are happy to announce that our paper Curiosities on the Monotone Preserving Cubic Splines has been accepted for publication in the Wilmott Magazine.
The content of the paper is nicely summarised by the starting paragraph of the referee report: "The authors have two results. The first is a worthwhile observation that the Hyman constraint is automatically satisfied, and can thus be omitted. The second is a sensitivity calculation. These results deserve to be published ..".
Needless to say, we are happy for such an achievement and proud to get recognition for the quality of our research from an international refereed journal. This is for us a confirmation of our capacities and an additional boost of motivation.
A working version of the paper can be found in our library page. The final publication can be obtained directly from the Technical Papers section of the Wilmott Magazine journal here.
A Credit Default Swaps (CDS) is a derivative to transfer default risk from one party to the next. The default protection is granted on the reference entity which can in principal be any entity, for example a single company, a group of companies or even a country. The protection buyer makes (quarterly) payments as compensation for the protection until either the end of the contract or the moment of default of the reference entity. This structure results in the pricing of this leg containing a part for the value of the payout in case of default and a part for the accrued premium until default. This side of the swap is called the premium leg.
The protection seller pays out a fixed amount in case of default of the reference entity. This amount is usually quoted as the notional amount times a recovery fraction. This side of the swap is called the protection leg.
To get a feel for the pricing of these kind of swaps please consider the simple attached example based on the book of Hull. In this example the CDS price is computed based on deterministic default probabilities and a fixed interest rate. To get a more realistic pricing, we could change the fixed interest rate with an interest rate model and the deterministic default probability with a stochastic model. However, that aside, we think this example gives a good basic understanding of how a CDS works.
The CDS example spreadsheet is available here : cds example
For a recent project we created an online house pricer for the Dutch market, Huizen Prijs Checker. The backend, a statistical model, was built using Java which connects to our PHP / WordPress frontend using an API. We have worked with WordPress before, but once again we were surprised to see how easy it’s to setup and customise using templates and plug-ins.
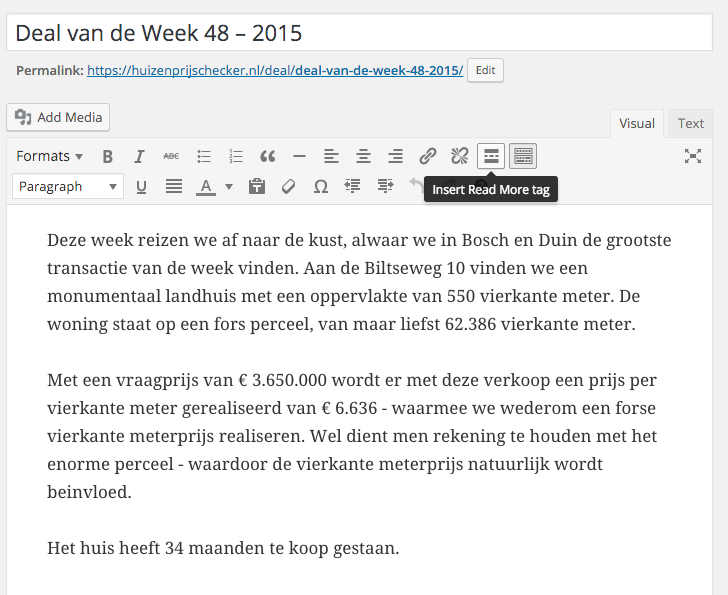
The site being local to Dutch market is all in Dutch. This meant creating pages and blogs in Dutch. Which works wonderfully. The one thing which gave us headache was the continue reading text displayed by the more-link object. The tag is inserted using the WordPress editor as shown here:
On your blog-role or category pages a link will be displayed with the text “Continue reading ->”, like so:
This wasn’t any good as our site was meant to be in Dutch. So we where hoping for something like:
It took quite some time to figure out how to get our theme to display a “continue reading” link with custom text. As it turns out this can be fixed by creating a child package. Details on how to do this can be found in WordPress Codex. Once you have the child theme setup the link text can be modified by adding a new read_more_link function to the functions.php file in your theme. This function will then override the default behaviour of the links. The following snippet does the trick. Continue reading
We have recently started the project of including the multi-curve framework into the UDFinLib, our own financial library. The topic is delicate, as it consists of both research and implementation at once.
After the 2007-2008 world financial crisis it became clear that the classical single-curve framework that had been used until then was not appropriate to value products and to hedge portfolio's positions. All of a sudden credit risk was an every day's topic, collateral margins exploded and the previously small spreads between different-tenor swaps (OIS vs Libor, 3M-tenor vs 6M-tenor) could not be neglected anymore. Single-curve building, which treated instrument with different tenors in the same way, had to be upgraded to multi-curve.
In a nutshell, the multi-curve framework amounts to construct one discount curve and many tenor curves. The discount curve is typically built with OIS instruments, which are the best approximation for the risk free rate. All the other tenor curve are built with instruments with homogeneous tenors. The most used tenors are 3M, 6M, 9M, 12M. Typically, the longer the tenor the riskier the trade and hence the higher the corresponding rate.
In this blog we give a non-exhaustive list of references that helped us in both understanding the multi-curve and designing the process.
Articles
Books
Nice reading!
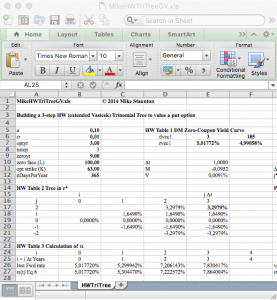
In a previous blog we presented an implementation of the Generalised Hull-White model (2014). This implementation relies on a numerical root-finding routine to determine model parameters so that model prices match actual market prices. The root finding is far from trivial as different algorithms will give different results. Fortunately the quality of the result can be easily monitored as the difference between model prices and actual marked prices is a clear indicator. As it turns out in most cases, the root finding for theta is not required. Instead an analytical formula can be used. Mike Staunton very kindly pointed us to a paper by Grant & Vora (2001) that shows that the approximation used by Hull-White is not necessary. The equations explained in the paper are implemented in the attached spreadsheet by Mike Stauton for the first 3 steps of the lattice giving a good example of how the process for finding theta works in practice.
The spreadsheet is available here:
References:
Grant & Vora (2001) , An Analytical Implementation of the Hull and White Model
http://janroman.dhis.org/finance/Hull%20&%20White/analytical-approximation-hull-and-white.pdf
Hull & White (2014), A Generalized Procedure for Building Trees for the Short Rate and its
Application to Determining Market Implied Volatility Functions
http://www-2.rotman.utoronto.ca/~hull/downloadablepublications/TreeBuilding.pdf